LoRA fine-tuning performance
Written on November 8th, 2023 by Jonathan Hilgart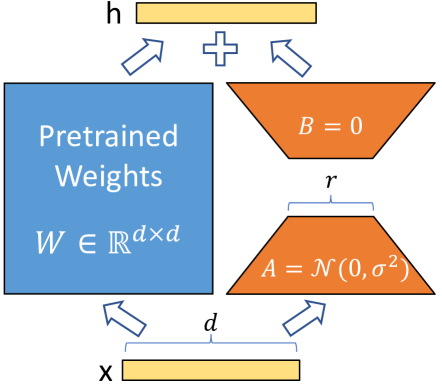
I recently went down the rabbit hole of trying to dig into:
- (1) How does LoRA stack up to full fine-tuning
- (2) How to serve multiple LoRA adapters
We’re just going to focus on the first point in this post as the SLoRA authors have effectively solved the multi-adapter serving challenge.
What is LoRA?
According to the paper LoRA can reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times. LoRA performs on-par or better than finetuning in model quality on RoBERTa, DeBERTa, GPT-2, and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency.. The way this is accomplished is through the training of low-rank weight matrices for the attention/mlp matrices in the LLM.
Here are some of the key parameters used in LoRA.
| Parameter | What is it | Typical Values | How to Set |
|---|---|---|---|
| r | Rank of LoRA matrices | 8, 16, … up to 256 | Larger is better as long as alpha is ~2x r |
| alpha | Alpha is needed for scaling updates | 16, 32, up to 512 | For LLMs, 2x the value of r |
| Quantized LoRA | Move from 16 bit to 8 bit | n/a | n/a |
| target_modules | Which layers to use LoRA matrices for | Most people use at least K and V matrices. Can use k, v, head, MLP, projection matrices (see here). | Using more layers = more memory but also better performance generally |
| dropout | Per layer, regularizer |
One of the biggest questions regarding LoRA has been whether the performance is comparable to full fine-tuning of all the weights. I consolidate the data from this post into the chart below. In addition, I’ve included some experiemnts to validate the post’s finding.
Performance for Llama 7B FP16 A100 40GB machine
| Row # | Model Type | r | Target Layers | Trainable Parameters / % of Original | GPU Mem Required for LoRA | Relative Performance (w/ best alpha) | Number of Adapters You Can Fit in Mem on A100 40GB Machine |
|---|---|---|---|---|---|---|---|
| 1 | Base model llama 7b | n/a | n/a | n/a | 15.5GB | 0.439 | n/a |
| 2 | * LoRA for performance numbers * LoRA for memory numbers | 8 | “V_proj” “q_proj” | ~4M / 0.1% | ~8 mb | 0.432 not directly comparable to above as this included additional fine tuning | n/a |
| 3 | * QLoRA for performance numbers * LoRA for memory numbers | 8 | “V_proj” “q_proj” | ~4M / 0.1% | ~8 mb | 0.42 | ~2k |
| 4 | * QLoRA for performance numbers * LoRA for memory numbers | 128 | “V_proj” “q_proj” | ~67M / 1% | ~130mb | n/a | ~180 |
| 5 | * QLoRA for performance numbers * LoRA for memory numbers | 256 | “V_proj” “q_proj” | ~134M / 2% | ~260mb | n/a | ~90 |
| 6 | * QLoRA for performance numbers * LoRA for memory numbers | 8 | “q_proj”, “up_proj”, “o_proj”, “k_proj”, “down_proj”, “gate_proj”, “v_proj” | ~20M / 0.3% | ~50 MB | 0.4478 | ~450 |
| 7 | * QLoRA for performance numbers * LoRA for memory numbers | 128 | “q_proj”, “up_proj”, “o_proj”, “k_proj”, “down_proj”, “gate_proj”, “v_proj” | ~320M / 4.5% | ~700mb | 0.4491 | ~30 |
| 8 | * QLoRA for performance numbers * LoRA for memory numbers | 256 | “q_proj”, “up_proj”, “o_proj”, “k_proj”, “down_proj”, “gate_proj”, “v_proj” | ~640M / 9% | ~1.6 GB | 0.459 | ~15 |
Summary
- LoRA vs baseline model, row 1 vs 2, are fairly comparable .2% delta
- LoRA vs QLoRA, row 2 vs 3, sees a 3% performance decrease
- As seen above, using LoRA on k and v to all layers, row 3 vs 6, for LoRA improves performance by ~7% but increases memory required by 6x.
- Increasing r for all layers for LoRA, the low rank factor, from 8 to 256 (row 6 vs 8), improves performance by 2.5% and increases memory required by ~32x.
We’ve also seem some support for alpha=2r with eval scores below.
- .783 LoRA average for validation score
- .7994 for LoRA alpha=2r for validation score
